FabCon is coming to Atlanta
Join us at FabCon Atlanta from March 16 - 20, 2026, for the ultimate Fabric, Power BI, AI and SQL community-led event. Save $200 with code FABCOMM.
Register now!- Power BI forums
- Get Help with Power BI
- Desktop
- Service
- Report Server
- Power Query
- Mobile Apps
- Developer
- DAX Commands and Tips
- Custom Visuals Development Discussion
- Health and Life Sciences
- Power BI Spanish forums
- Translated Spanish Desktop
- Training and Consulting
- Instructor Led Training
- Dashboard in a Day for Women, by Women
- Galleries
- Data Stories Gallery
- Themes Gallery
- Contests Gallery
- QuickViz Gallery
- Quick Measures Gallery
- Visual Calculations Gallery
- Notebook Gallery
- Translytical Task Flow Gallery
- TMDL Gallery
- R Script Showcase
- Webinars and Video Gallery
- Ideas
- Custom Visuals Ideas (read-only)
- Issues
- Issues
- Events
- Upcoming Events
The Power BI Data Visualization World Championships is back! Get ahead of the game and start preparing now! Learn more
- Power BI forums
- Forums
- Get Help with Power BI
- DAX Commands and Tips
- Multiparent Graph, Recursiveness
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Multiparent Graph, Recursiveness
Hi community,
I am addressing the following issue, stemming from 2 observations concerning graph structures in DAX:
- The build in PATH function does not support several parents for one child.
- DAX is not recursive. This means that the implementation of graph exploration strategies starting with only e.g., an adjacency list is not possible in DAX
My business problem is simple to understand: in a hierarchical company structure revenue of a child organization is recognized for several parents. A common application would be bonus agreements, where employees get bonus payments for revenues in child organizations. These bonus agreements cover then a completely internal structure which has nothing to do with the structure of the legal entities of the company, they rather are arbitrary.
For these reasons I executed the entire graph search in Power Query and then handed over the result for visualization. The approach is outlined below.
I have then several questions, where I would like your help:
- in the approach below, are there elements which can be replaced by features that are out of the box either in Power Query or DAX?
- If not, is there a pattern here, where necessarily recursive work is executed in Power Query and then handed over to the Vertipaq engine?
- Are there any performance concerns when doing so?
Approach:
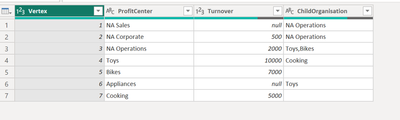
We have as toy model a turnover table which specifies the turnover in the period and the child organizations.
Organizations can have turnover or not (if they are pure umbrella organizations they do not). The real model has over 100 organizations and ideally, we explore the graph to get the dept of graph and do not put in this information beforehand. Therefore, the algorithm must be recursive.
This is results in the following adjacency list:
{{1,{3}},{2,{3}},{3,{4,5}},{4,{7}},{5,{}},{6,{4}},{7,{}}}
Now some standard Depth First Search (DFS) is applied:
DFS = (adjacencyList as list, visited as list, queue as list) =>
let
result = if List.NonNullCount(queue) = 0
then visited
else
let
v = Pop(queue){0},
restQueue = Pop(queue){1},
children = GetNeighbours(adjacencyList, v)
in
if List.Contains(visited, v)
then @DFS(adjacencyList, visited, restQueue)
else @DFS(adjacencyList, List.Combine ({ {v}, visited}), List.Combine({restQueue ,children}))
in
result
All vertices are taken and the children are determined:
GetDescendants = (adjacencyList as list, v as number) =>
let
children = GetNeighbours(adjacencyList, v ),
result = DFS(adjacencyList, {}, children)
in
result
with
GetNeighbours = (adjacencyList as list, v as number) =>
let
selection = List.Select(adjacencyList, (x) => x{0} = v),
result = if List.Count(selection) > 0 then selection{0}{1} else {}
in
result
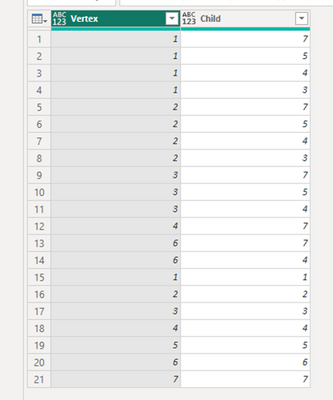
The output can be transformed into a table with the added feature that a vertex is its own child.
let
Vertices = Table.SelectColumns(Turnover, "Vertex"),
Descendants = Table.AddColumn(Vertices, "Col1",
each
let
v = [Vertex],
children = GetNeighbours(TurnoverTree, [Vertex]),
result = {v, GetDescendents(TurnoverTree, v)}
in
result),
ls1 = Table.Column(Descendants, "Col1"),
ls2 = List.Transform(ls1, (ls) =>
let
v = ls{0},
n = List.Count(ls{1}),
elementToAdd = if n > 0 then
let
generator = List.Repeat({v},n),
zip = List.Zip({generator, ls{1}})
in
zip
else {}
in
elementToAdd),
ls3 = List.Combine(ls2),
ls4 = List.Transform(Table.Column(Vertices, "Vertex"), (x) => {x,x}),
ls5 = List.Combine({ls3, ls4}),
tab = #table( {"Vertex", "Child"}, ls5)
in
tab
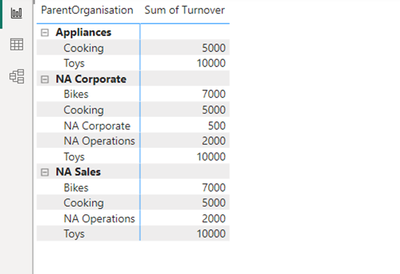
The rest is then straight forward. We can now assign now turnovers to the parents and have a completely basic unformatted visual like this (a nice visual is not the point of the question)
Again, my key questions are:
- In the approach above, are there elements which can be replaced by features that are out of the box either in Power Query or DAX?
- If not, is there a pattern here, where necessarily recursive work is executed in Power Query and then handed over to the Vertipaq engine?
- Are there any performance concerns when doing so?
Thank you for your help.
Best regards
Christian
Helpful resources

Power BI Dataviz World Championships
The Power BI Data Visualization World Championships is back! Get ahead of the game and start preparing now!

| User | Count |
|---|---|
| 19 | |
| 13 | |
| 8 | |
| 4 | |
| 4 |
| User | Count |
|---|---|
| 29 | |
| 22 | |
| 17 | |
| 11 | |
| 10 |