FabCon is coming to Atlanta
Join us at FabCon Atlanta from March 16 - 20, 2026, for the ultimate Fabric, Power BI, AI and SQL community-led event. Save $200 with code FABCOMM.
Register now!- Power BI forums
- Get Help with Power BI
- Desktop
- Service
- Report Server
- Power Query
- Mobile Apps
- Developer
- DAX Commands and Tips
- Custom Visuals Development Discussion
- Health and Life Sciences
- Power BI Spanish forums
- Translated Spanish Desktop
- Training and Consulting
- Instructor Led Training
- Dashboard in a Day for Women, by Women
- Galleries
- Data Stories Gallery
- Themes Gallery
- Contests Gallery
- QuickViz Gallery
- Quick Measures Gallery
- Visual Calculations Gallery
- Notebook Gallery
- Translytical Task Flow Gallery
- TMDL Gallery
- R Script Showcase
- Webinars and Video Gallery
- Ideas
- Custom Visuals Ideas (read-only)
- Issues
- Issues
- Events
- Upcoming Events
The Power BI Data Visualization World Championships is back! Get ahead of the game and start preparing now! Learn more
- Power BI forums
- Forums
- Get Help with Power BI
- DAX Commands and Tips
- Re: DAX Polynomial Regression Calculation Issue
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
DAX Polynomial Regression Calculation Issue
I am attempting to implement a 2nd order polynomial regression to fit some data. It appears that I can calculate the coefficients for the regression equation correctly, but I just cannot figure out how to correctly return the correct result of the equation to use in a table/chart. Starting from this solution, I ended up with the following measure:
values (poly fit) =
// Reference: https://www.thedatascientists.com/polynomial-regression/
// https://metric.ma.ic.ac.uk/metric_public/matrices/inverses/inverses2.html
// Because our Xs (dates) and Ys (measures) are in different tables, we have to temporarily create a new table (Known) with both of those values so we can perform SUMX operations easily.
// To get the same polynomial fit as excel, the x values in the calculation are masked over with 1 thru n. Thus x-values in the calc are n+1-min(n)
var countItems = COUNTX(VALUES(Table1[date]),Table1[date])
var Known =
SELECTCOLUMNS (
ALLSELECTED(Table1[date]),
"KnownX", [zSequence1ToN],
"KnownY", CALCULATE(SUMX(Table1,[values]))
)
var sumOfXs = SUMX(Known, [KnownX])
var sumOfYs = SUMX(Known, [KnownY])
var sumOfX2 = SUMX(Known, [KnownX] ^ 2)
var sumOfX3 = SUMX(Known, [KnownX] ^ 3)
var sumOfX4 = SUMX(Known, [KnownX] ^ 4)
var sumOfXY = SUMX(Known, [KnownX] * [KnownY])
var sumOfX2Y = SUMX(Known, [KnownX] ^ 2 * [KnownY])
var determinant = countItems*((sumOfX2*sumOfX4)-(sumOfX3*sumOfX3))-sumOfXs*((sumOfXs*sumOfX4)-(sumOfX2*sumOfX3))+sumOfX2*((sumOfXs*sumOfX3)-(sumOfX2*sumOfX2))
//Calculate the inverse matrix (combining a few steps together)
var M11 = ((sumOfX2*sumOfX4)-(sumOfX3*sumOfX3))/determinant
var M12 = -((sumOfXs*sumOfX4)-(sumOfX3*sumOfX2))/determinant
var M13 = -((sumOfX2*sumOfX2)-(sumOfXs*sumOfX3))/determinant //there was an error on this line i had to add a negative to fix. no idea why. EVERY other var evaluates correctly.
var M21 = -((sumOfXs*sumOfX4)-(sumOfX2*sumOfX3))/determinant
var M22 = ((countItems*sumOfX4)-(sumOfX2*sumOfX2))/determinant
var M23 = -((countItems*sumOfX3)-(sumOfXs*sumOfX2))/determinant
var M31 = ((sumOfXs*sumOfX3)-(sumOfX2*sumOfX2))/determinant
var M32 = -((countItems*sumOfX3)-(sumOfX2*sumOfXs))/determinant
var M33 = ((countItems*sumOfX2)-(sumOfXs*sumOfXs))/determinant
//Assuming equation of: a*x^2 + b*x + c
var c = M11*sumOfYs+M12*sumOfXY+M13*sumOfX2Y
var b = M21*sumOfYs+M22*sumOfXY+M23*sumOfX2Y
var a = M31*sumOfYs+M32*sumOfXY+M33*sumOfX2Y
RETURN
// SUMX(
// DISTINCT(Table1[date]),
// a * [zSequence1ToN] ^ 2 + b * [zSequence1ToN] + c
// )
[a]*[zSequence1ToN]^2+[b]*[zSequence1ToN]+[c]
Where [zSequence1ToN] is a RANKX of the date values
zSequence1ToN = RANKX(ALLSELECTED(Table1[date]),CALCULATE(SUM(Table1[date])),,ASC)
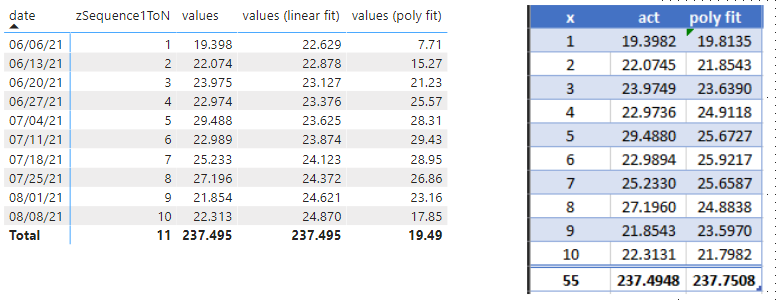
My issue is I cannot figure out how to correctly calculate this for each row in the table. The screenshot below is what I am getting (compared to what I should be getting - at least according to excel.
I suspect my issue may be where I am returning the values, but at this point I am out of ideas and need advice. I have attached a sample pbix file and the excel file I was using for validation. What am I doing wrong?
https://1drv.ms/u/s!Ah3VDq5HnODQgcArelYadi0cXQQZzA?e=8YdvQK
Solved! Go to Solution.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I think the main problem here is this: COUNTX(VALUES(Table1[date]),Table1[date])
This is evaluated within the local filter context and returns 1 for each row corresponding to a single date.
Try this instead: COUNTROWS ( ALLSELECTED ( Table1[date] ) )
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Hi, PLEASE HELP!!
I'm prototyping a similar calculation in excel for a 4th order polynomial with a 5x5 matrix, but I cannot seem to generate the same result as LINEST() in excel, see attached....
https://1drv.ms/x/s!AsId0OAmsuzuhOEh7CR03iyUCLAbng?e=fiK5ay
I've used the Chio method of expansion to compute the determinant...
https://www.youtube.com/watch?v=_JetUVpvFAU
I've then computed matrix of minors and matrix of cofactors to work out the inverse of the original 5x5 matrix, as instructed here...
https://www.mathsisfun.com/algebra/matrix-inverse-minors-cofactors-adjugate.html
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Found a solution for a 5x5 matrix using Chio method of expansion and Cramer's Rule, parsing the solution vector into a series of matrices, to calculate determinants divided by the original determinant to solve for the polynomial regression coefficients...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I have a matrix with 2 columns from which i want to run a polynomial regression to the fourth degree to fit a line on data. The fourth degree is to smooth the data basically looking at daily data with a smoothing effect over a four week period. I can't seem to convert the equations of the DAX code above to give me the results of a fourth degree and struggling to convert your excel spreadsheet to those equations. Any help would be greatly appreciated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
I think the main problem here is this: COUNTX(VALUES(Table1[date]),Table1[date])
This is evaluated within the local filter context and returns 1 for each row corresponding to a single date.
Try this instead: COUNTROWS ( ALLSELECTED ( Table1[date] ) )
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Thank you for your input, however that did not seem to have any effect. Would that have an effect on the final return result if that var only returns a single number of the count?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
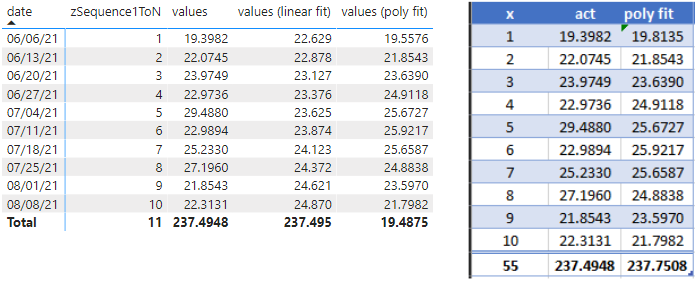
This is what I get when I make that change:
Good match except for x = 1.
Note that you need to make the same change for each of [a], [b], [c] or else change your final line of [values (poly fit)] to a*[zSequence1ToN]^2+b*[zSequence1ToN]+c (use the variables you've already computed instead of referencing other measures).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
That's a facepalm moment. I was indeed using the measures instead of the variables. Thanks!
So the moral of the story is that local filter context is passed down through dependent variables too. That is something I would not have considered.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Report Inappropriate Content
Yes. Each VAR is calculated within the local filter context.
Helpful resources

Power BI Monthly Update - November 2025
Check out the November 2025 Power BI update to learn about new features.

Fabric Data Days
Advance your Data & AI career with 50 days of live learning, contests, hands-on challenges, study groups & certifications and more!

| User | Count |
|---|---|
| 21 | |
| 10 | |
| 9 | |
| 4 | |
| 4 |
| User | Count |
|---|---|
| 34 | |
| 31 | |
| 20 | |
| 13 | |
| 12 |