F.DIST 08-31-2021 05:10 AM

[Greg_Deckler]

In my recent quest to create or catalog as many DAX equivalents for Excel functions was able to leverage my work on GAMMA to come up with F.DIST.

F.THIS = 
    VAR __x = [x]
    VAR __Deg1 = [Deg_freedom1]
    VAR __Deg2 = [Deg_freedom2]
    VAR __GAMMA1 = 
        VAR __zInput = (__Deg2 + __Deg1) / 2
        VAR __p =
            {
                (0, 676.5203681218851),
                (1, -1259.1392167224028),
                (2, 771.32342877765313),
                (3, -176.61502916214059),
                (4, 12.507343278686905),
                (5, -0.13857109526572012),
                (6, 9.9843695780195716e-6),
                (7, 1.5056327351493116e-7)
            }
        VAR __EPSILON = 1e-7
        VAR __z = IF(__zInput < 0.5, 1 - __zInput - 1,__zInput - 1)
        VAR __pTable = 
            ADDCOLUMNS(
                __p,
                "x",[Value2] / (__z + [Value1] + 1)
            )
        VAR __x = 0.99999999999980993 + SUMX(__pTable,[x])
        VAR __t = __z + COUNTROWS(__pTable) - .5
        VAR __y = 
            IF(
                __zInput < 0.5,
                PI() / (SIN(PI() * __zInput) * SQRT(2*PI()) * POWER(__t,__z+0.5) * EXP(-1*__t) * __x),
                SQRT(2*PI()) * POWER(__t,__z+0.5) * EXP(-1*__t) * __x
            )
    RETURN
        __y
    VAR __GAMMA2 = 
        VAR __zInput = (__Deg1) / 2
        VAR __p =
            {
                (0, 676.5203681218851),
                (1, -1259.1392167224028),
                (2, 771.32342877765313),
                (3, -176.61502916214059),
                (4, 12.507343278686905),
                (5, -0.13857109526572012),
                (6, 9.9843695780195716e-6),
                (7, 1.5056327351493116e-7)
            }
        VAR __EPSILON = 1e-7
        VAR __z = IF(__zInput < 0.5, 1 - __zInput - 1,__zInput - 1)
        VAR __pTable = 
            ADDCOLUMNS(
                __p,
                "x",[Value2] / (__z + [Value1] + 1)
            )
        VAR __x = 0.99999999999980993 + SUMX(__pTable,[x])
        VAR __t = __z + COUNTROWS(__pTable) - .5
        VAR __y = 
            IF(
                __zInput < 0.5,
                PI() / (SIN(PI() * __zInput) * SQRT(2*PI()) * POWER(__t,__z+0.5) * EXP(-1*__t) * __x),
                SQRT(2*PI()) * POWER(__t,__z+0.5) * EXP(-1*__t) * __x
            )
    RETURN
        __y
    VAR __GAMMA3 = 
        VAR __zInput = (__Deg2) / 2
        VAR __p =
            {
                (0, 676.5203681218851),
                (1, -1259.1392167224028),
                (2, 771.32342877765313),
                (3, -176.61502916214059),
                (4, 12.507343278686905),
                (5, -0.13857109526572012),
                (6, 9.9843695780195716e-6),
                (7, 1.5056327351493116e-7)
            }
        VAR __EPSILON = 1e-7
        VAR __z = IF(__zInput < 0.5, 1 - __zInput - 1,__zInput - 1)
        VAR __pTable = 
            ADDCOLUMNS(
                __p,
                "x",[Value2] / (__z + [Value1] + 1)
            )
        VAR __x = 0.99999999999980993 + SUMX(__pTable,[x])
        VAR __t = __z + COUNTROWS(__pTable) - .5
        VAR __y = 
            IF(
                __zInput < 0.5,
                PI() / (SIN(PI() * __zInput) * SQRT(2*PI()) * POWER(__t,__z+0.5) * EXP(-1*__t) * __x),
                SQRT(2*PI()) * POWER(__t,__z+0.5) * EXP(-1*__t) * __x
            )
    RETURN
        __y
RETURN
    DIVIDE(__GAMMA1,__GAMMA2 * __GAMMA3) * 
        POWER(__Deg1/__Deg2,__Deg1/2) *
            DIVIDE(
                POWER(__x,(__Deg1-2)/2),
                POWER(1+(__Deg1/__Deg2)*__x,(__Deg1+__Deg2)/2)
            )

The cumulative form of F.DIST is:

F.THIS.CUMULATIVE = 
    VAR __x = [x]
    VAR __df1 = [Deg_freedom1]
    VAR __df2 = [Deg_freedom2]
RETURN
    BETA.DIST(
        __x*__df1/(__x*__df1+__df2),
        __df1/2,
        __df2/2,
        TRUE
    )

F.DIST.RT is:

F.THIS.RT = 1 - [F.THIS.CUMULATIVE]

F.INV is this:

F.INV = 
    VAR __p = [F.THIS.CUMULATIVE]
    VAR __df1 = [Deg_freedom1]
    VAR __df2 = [Deg_freedom2]
RETURN
    BETA.INV(__p,__df1/2,__df2/2) * __df2/(__df1*(1-BETA.INV(__p,__df1/2,__df2/2)))

And last but not least, F.INV.RT:

F.INV.RT = 
    VAR __p = 1 - [F.THIS.RT]
    VAR __df1 = [Deg_freedom1]
    VAR __df2 = [Deg_freedom2]
RETURN
    BETA.INV(__p,__df1/2,__df2/2) * __df2/(__df1*(1-BETA.INV(__p,__df1/2,__df2/2)))

Thank goodness for actual documentation:

• https://support.minitab.com/en-us/minitab-express/1/help-and-how-to/basic-statistics/probability-dis...
• http://www.real-statistics.com/chi-square-and-f-distributions/f-distribution/

eyJrIjoiOGRlZDc0OTUtMjE3MC00Mjg4LTgxZTktMDEzMDkxNzEzZjUxIiwidCI6IjRhMDQyNzQzLTM3M2EtNDNkMi04MjdiLTAwM2Y0YzdiYTFlNSIsImMiOjN9

[MJEnnis]

This is pretty awesome! I thought it was weird that PowerBI has functions for the Beta distribution, but not the F distribution. I spent a few hours reflecting on how to use the T distribution or Beta distribution functions to calcuate F.INV. I needed it desparately to dynamically calculate confidence intervals to report a measure of interclass correlation. I was just about to give up and write a complaint to Microsoft when I stumbled upon this great post! Thanks a lot, @Greg_Deckler! This is not the first time you have helped me through such problems!

[MJEnnis]

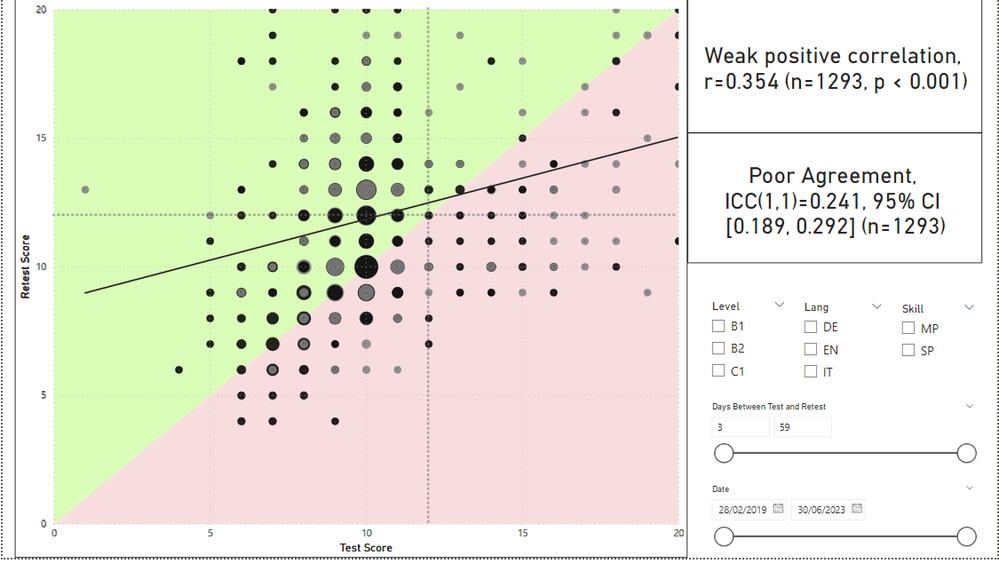
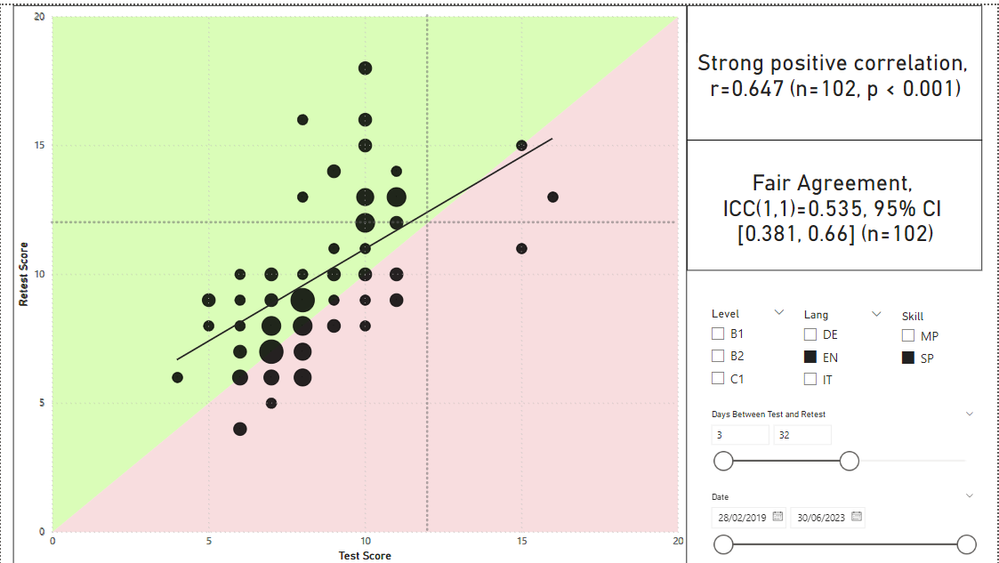
Pasting in an example of the F.INV measure being used in a report to calculate the confidence intervals for an interclass correlation coefficient. Pretty cool to get a dynamic calcuation that works with filters!

No filter appliedMultiple filters applied

[MJEnnis]

And here is the code to calculate ICC with interpretation and confidence intervals. 

Test_Retest_ICC = 

VAR n = COUNTROWS('TEST_RETEST')
VAR nT = n*2

VAR k = 2

VAR AvgT = DIVIDE(SUM('TEST_RETEST'[Test Score]) + SUM('TEST_RETEST'[Retest Score]),nT)

VAR SST = SUMX('TEST_RETEST', ('TEST_RETEST'[Test Score]-AvgT)*('TEST_RETEST'[Test Score]-AvgT)) + SUMX('TEST_RETEST', ('TEST_RETEST'[Retest Score]-AvgT)*('TEST_RETEST'[Retest Score]-AvgT))

VAR SSW = SUMX('TEST_RETEST', 
('TEST_RETEST'[Test Score]-DIVIDE('TEST_RETEST'[Retest Score]+'TEST_RETEST'[Test Score],k)) * 
('TEST_RETEST'[Test Score]-DIVIDE('TEST_RETEST'[Retest Score]+'TEST_RETEST'[Test Score],k)) + 
('TEST_RETEST'[Retest Score]-DIVIDE('TEST_RETEST'[Retest Score]+'TEST_RETEST'[Test Score],k)) * 
('TEST_RETEST'[Retest Score]-DIVIDE('TEST_RETEST'[Retest Score]+'TEST_RETEST'[Test Score],k)))

VAR SSB = SST-SSW

VAR DFW = (n*k)-n
VAR DFB = n-1

VAR MSB=DIVIDE(SSB,DFB)
VAR MSW=DIVIDE(SSW,DFW)

VAR ICC = (MSB-MSW)/(MSB+((k-1)*MSW))

Var CCT = 
SWITCH(TRUE,
       ICC>=-1 &&  ICC<0 ,"Invalid Estimate",
        ICC=0                           ,"No Agreement",
        ICC>0    &&  ICC<0.4   ,"Poor Agreement",
        ICC>=0.4 &&  ICC<0.6   ,"Fair Agreement",
        ICC>=0.6 &&  ICC<0.75   ,"Good Agreement",
        ICC>=0.75 &&  ICC<1   ,"Excellent Agreement",
        ICC=1                           ,"Perfect Agreement"
)

VAR F = MSB/MSW

VAR alpha = 0.05
VAR alpha_Tail = alpha/2

/* The next two variables are taken from the F.INV measure provided by Greg. Ideal to report confidence intervals with the ICC, and you need F.INV to calculate those. This is but just one example of a practical application of Greg's measure. It can also be used for ANOVA stats, for example. Until the PBI developers add F.DIST and F.INV DAX functions, I will be borrowing this measure!  */

VAR FINV_L = BETA.INV(1-alpha_Tail,DFB/2,DFW/2)  * DFW/(DFB*(1-BETA.INV(1-alpha_Tail,DFB/2,DFW/2)))
VAR FINV_U = BETA.INV(1-alpha_Tail,DFW/2,DFB/2)  * DFB/(DFW*(1-BETA.INV(1-alpha_Tail,DFW/2,DFB/2)))

VAR F_L = DIVIDE(F,FINV_L)
VAR F_U = F*FINV_U

VAR LOWER_ = DIVIDE(F_L-1,F_L+k-1)
VAR UPPER_ = DIVIDE(F_U-1,F_U+k-1)


RETURN CCT & ", ICC(1,1)=" & ROUND(ICC,3) & ", 95% CI [" & ROUND(LOWER_,3) & ", " & ROUND(UPPER_,3) &"]" & " (n=" & n & ")"

[Barendnu]

Thank you very much! I was looking for the equivalent of Statistics.FDistribution in DAX, and this works great, very handy indeed!